微环谐振腔中的耗散椭圆余弦波(Turing rolls)和孤子极限

单孤子是一般波的一种特殊极限，通常称为椭圆余弦波或图灵卷。来自美国马里兰大学的研究人员们从理论上和计算上研究了微谐振腔中椭圆余弦波的稳定性和可获得性。研究人员们证明了它们的鲁棒性，并且与单孤子相比，在大多数情况下可以很容易且确定地访问它们。它们的带宽可以与单个孤子相比较，在这种情况下，它们实际上是一个周期的孤子序列，并且与一个功率增加的频率梳相对应。研究人员们综合研究了失谐、泵浦振幅和振型周长组成的三维参数空间，以确定稳定解存在的位置。为了完成这项任务，他们使用了一套独特的基于动力系统理论的计算工具，从而能够快速准确地确定每个椭圆余弦波周期的稳定区域，并找到不稳定机制及其时间尺度。最后，研究人员们重点研究了孤子极限，结果表明，对于连续波和多个高周期椭圆余弦波，即多个有效的孤子序列，单孤子的稳定区域几乎完全重合。这一结果在一定程度上解释了为什么很难确定地获得单个孤子。

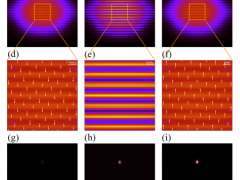
图：由所有可能的波形组成的相空间中引力池的示意图。如果初始条件(如红点所示)从静止波形的吸引盆内开始(如灰色所示)，则解将收敛到静止解。如果初始条件是从盆地外部开始的，如蓝点所示，那么解就会演化为另一个稳定解，或者永远不会成为稳定解。