双半子结构光：超越斯格明子的全新光学拓扑态

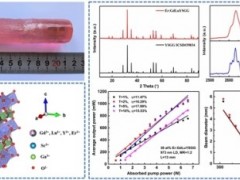
       近日，来自于英国南安普顿大学的高级研究员申艺杰博士在理论上提出了一种结构光的全新拓扑态——双半子（bimeron），这是一种打破斯格明子（skyrmion）拓扑态限制的广义准粒子态。本文构建的矢量光束在其偏振斯托克斯矢量场完美模拟了双半子的粒子结构，它可以具有可控的拓扑数，揭示了比光学斯格明子态更广泛的拓扑变换性质。相关工作“Topological bimeronic beams”发表在光学权威期刊Optics Letters，并被评为编辑精选（Editor's Pick）文章。 

       在粒子物理和磁性介质领域中，具有复杂结构的拓扑准粒子在信息的处理与存储种有很大的潜力。其中最具代表性的自旋拓扑结构就是斯格明子。这是携带有非零拓扑荷的纳米级圆形畴壁。斯格明子最近在结构光学领域中提出，已经成为了拓扑光学领域一个重要的研究方向。研究人员已经发现了许多从斯格明子演化而来的自旋拓扑结构。双半子是利用斯格明子经过连续拓扑变换得到的，也可以看成是有两个极性不同的半斯格明子（又称半子）组合而成。双半子因相较于传统的斯格明子具有更加广泛的拓扑态已然在基础物理和磁性材料领域中扮演着重要的角色。但是，时至今日，光学中的尚未有相关报道。实现光学双半子的方法是利用特殊矢量结构光的叠加使得其在实空间中利用偏振斯托克斯矢量构建出与双半子结构相似的拓扑结构。双半子态的意义在于给结构光提供一种更广泛的拓扑调控，除此之外，本文提出类比于2D庞加莱球的新型图像化模型——3D庞加莱球用于表征双半子拓扑变换，并作为一种直观的工具指导之后的工作。此外，该光束传播的过程中，可以形成在理论上预测到出现多种拓扑态，这种3D矢量光束有着极其简洁而优雅的拓扑特征，满足如今对于高阶结构调控的迫切需求，同时保证了现代光学通信与加密对于更大带宽和以及在信息处理中更快速的要求。（SHEN LAB）

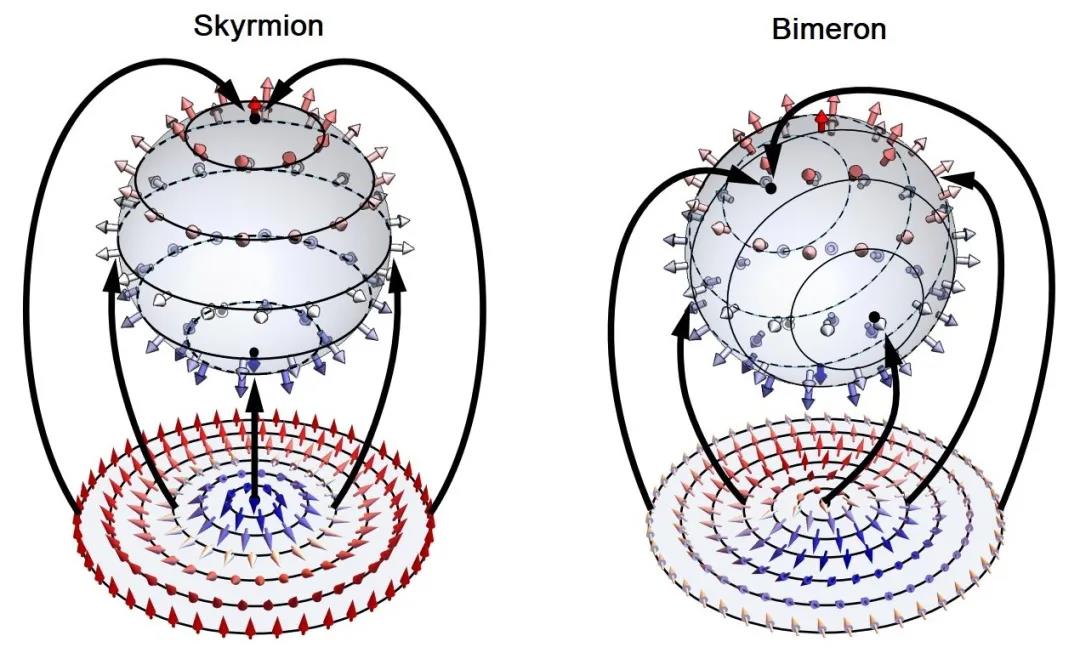
图1：斯格明子与双半子的表征。斯格明子可以被表示为一组在单位自旋球上的3D矢量展开到2D平面上。同理，双半子作为斯格明子的一种拓扑变换也可以利用同样的映射来表述，不过在映射的过程球上的经纬度进行了重整。

      文章链接:Y. Shen, "Topological bimeronic beams" Opt. Lett. 46(15), 3737-3740 (2021).(Editor’s Pick)