意大利佛罗伦萨大学Alessandro Zavatta课题组QUTE：以相干多模光子叠加法产生量子信息协议的非相关态

      最近发展起来的非局域单光子叠加技术被证明可能会产生多模光量子态的一种新的联合统计特性——非相关性，即每个模式中的光子数可以单独取任意值，但两个模式叠加在一起却永远不会表现出相同的结果。通过在不同时间模式下将一个单光子相干地加入到两个完全相同的相干光状态中，Nicola Biagi等人首次在实验上获得了非相关性的观测结果。操控这种统计属性的能力在包括不受信任方之间的信息安全分发等设想场景中将会有所应用，就像所谓的“精神扑克”游戏。

       当考虑到电磁场的不同模式时，填充在每个模式中的光子数（NoP）可能呈现出各种各样的分布。独立于每个单模式中的分布，不同模式中光子数之间的相关性特别令人感兴趣，并且可能存在不同的形式。在平衡光束分流器的一个输入端口中注入相干态光束，另一个端口中保持真空的情况下，在一个输出模式下观察到的特定光子数量n的概率独立于在另一个输出模式中观察到的相应光子数m的概率，即二者不相关（图1a）。如果一个经典的热状态被分裂，相关性将被观察到，此时在两种模式下测量相同NoP的概率更高。这些经典关联已经在鬼成像应用中得到了使用，而例如通过参数下转换产生的双光束中存在的非经典关联，已知可以为量子增强成像和传感带来额外和独特的优势。

       原则上，一个理想的双模压缩真空会显示出完美的光子数关联性，这意味着两个完美的探测器总是会在两个模式中测量出相同的光子数。这种完美关联性对于量子通信任务如双方必须共享共同但随机的信息也很重要。另一方面，当一个单光子被用在光束分流器的输入端时，输出端之间将观测到完美的反相关性，即如果一个单光子在一个输出端被测量到，则另一个输出端中没有光子存在，反之亦然。而在所谓的Hong-Ou-Mandel（HOM）方案中，两个不可区分光子撞击到平衡光束分流器上产生了相等的反相关性输出。

      与上述不同的是，Meyer-Scott等人最近讨论了不同场模式下NoP中的一种新形式的相关性。它包括在一种模式下对NoP的特定结果概率进行归零，而在另一种模式下对给定的测量结果进行归零。将其恰当地命名为非相关性，它表现在联合光子数概率分布pn1,n2的空元素中。特别地，pn,n=0的情况可以存在，其中在两种模式下测量相同光子数n的概率对于所有n始终为零，但是边缘分布pn=pn,0+pn,1+pn,2+...+pn,∞总是非零（图1b）。

        图1c给出了一种可视化不相关性的可替代方法。在这里，沿着联合光子数分布对角线方向的积分显示了两种模式之间的光子计数差值Δn=n1-n2的概率P(Δn)。因此，一个可分离状态（图1a）在Δn=0时显示最大值，然而理想的不相关态（图1b）在那里的值为零，这意味着在两种模式下测量相同数量的光子的可能性为零。

       与需要共享公共随机密钥的量子密钥分配方案相反，“不相关性”可用于在各方之间分配唯一的随机性。尤其是，它在所谓的“精神扑克”问题中很有用，该问题涉及到在没有可信任的第三方的情况下，远距离玩家之间的玩牌的公平性。

       Rivest、Shamir和Adleman（RSA）于1981年首次提出了一种解决这类问题的可能（经典）方案，该方案也与安全投票或电子现金的盲签名有关，这也是Alice和Bob作为两个不值得信任的当事人通过电话打扑克情景的首次出现之一。他们所提出的协议依赖于交换加密，即通过以不同顺序执行解密操作来正确检索多重加密消息的可能性。然而，与RSA公共密匙算法一样，该方案的安全性完全依赖于因式分解的数学问题的难度。相反地，共享一个不相关性的多模式状态将自然地保证分布式随机数的唯一性。

       这项工作的目的是为量子信息协议提供这种有价值的资源的第一个实验证据。

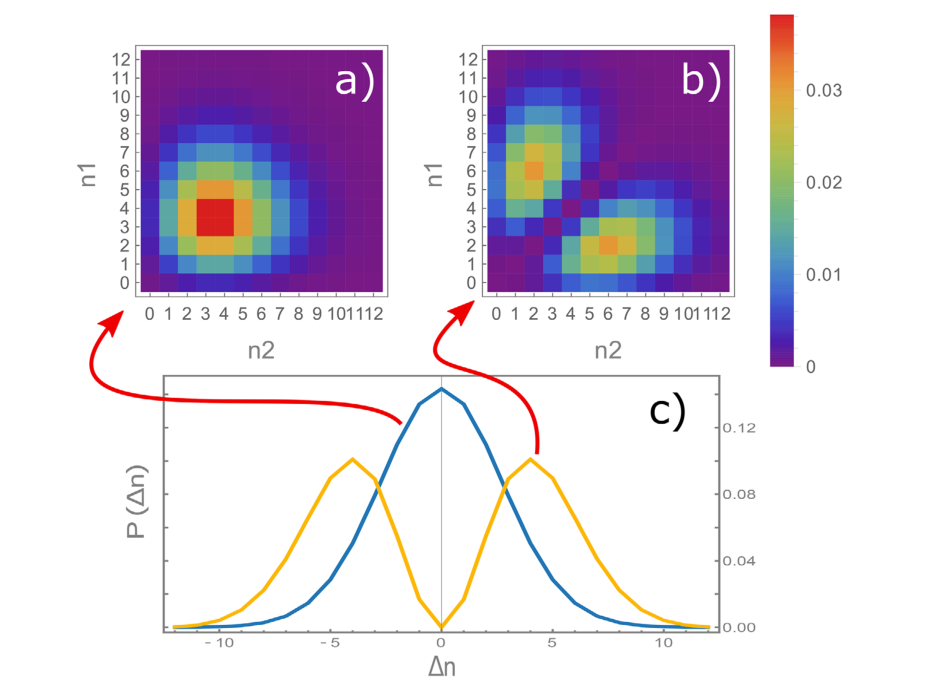
图1：以下状态中的联合光子数分布：a)理想的可分离的|α⟩1|α⟩2态（α= 2），例如通过在50％的光束分流器中分裂相干态|α⟩获得。在这种情况下，两种模式下测得的光子数不相关。b)在添加非局域单光子后，相同状态表现出非相关性;  c)沿上述联合光子数分布的对角线方向的积分（更多详细信息，请参见正文）

       总之，意大利佛罗伦萨大学Alessandro Zavatta课题组等人已经证明了他们最近发展的基于单光子非局域叠加的方法，除了允许纠缠任意大小尺寸的任意状态外，还可以产生非相关态。在含有全同、不相关的相干态的两个不同的传播时间模式上进行单光子叠加，导致它们的联合光子数分布不相关，即不可能在两个模式中测量相同的NoP。通过进行一个简化的双模层析重建工作，他们在实验上验证了不相关态的产生，这使得他们能够处理重建具有更大平均光子数的态时所增加的计算工作量。即使存在有限的检测效率、不完善的准备状态和统计噪声等问题，他们的实验结果仍然清楚地显示了不相关性的鲜明特征，即概率分布P(Δn)中心处的倾角，可以作为两种模式下光子计数差异的函数。

       在这里首次得到实验验证的不相关量子态的特殊统计性质可能会使得这些状态在新的特定应用中发挥作用。例如，在两方之间分配随机数同时确定其唯一性的可能性，即两方不可能收到相同的数字，可应用于分布式投票方案或“精神扑克”游戏中的公平卡牌交易。